Wavelet Transforms¶
New in version 0.9.1: Wavelet functions were only added in version 0.9.1
We are going to use wavelets to transform an image so that most of its values are 0 (and otherwise small), but most of the signal is preserved.
The code for this tutorial is avalailable from the source distribution as
mahotas/demos/wavelet_compression.py.
We start by importing and loading our input image
import numpy as np
import mahotas
import mahotas.demos
from mahotas.thresholding import soft_threshold
from matplotlib import pyplot as plt
from os import path
f = mahotas.demos.load('luispedro', as_grey=True)
f = f[:256,:256]
plt.gray()
# Show the data:
print("Fraction of zeros in original image: {0}".format(np.mean(f==0)))
plt.imshow(f)
plt.show()
(Source code, png, hires.png, pdf)
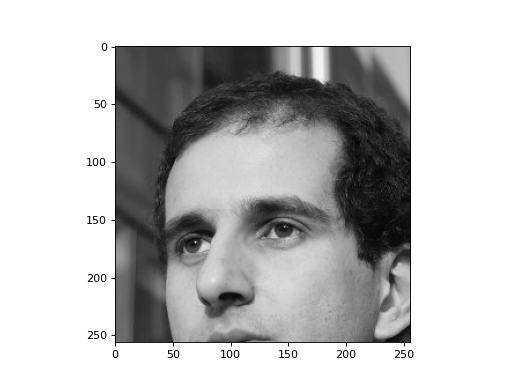
There are no zeros in the original image. We now try a baseline compression method: save every other pixel and only high-order bits.
direct = f[::2,::2].copy()
direct /= 8
direct = direct.astype(np.uint8)
print("Fraction of zeros in original image (after division by 8): {0}".format(np.mean(direct==0)))
plt.imshow(direct)
plt.show()
(Source code, png, hires.png, pdf)
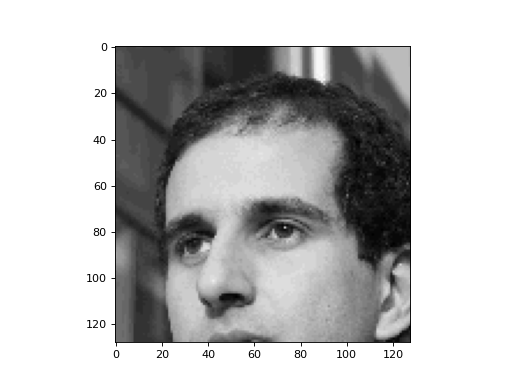
There are only a few zeros, though. We have, however, thrown away 75% of the values. Can we get a better image, using the same number of values, though?
We will transform the image using a Daubechies wavelet (D8) and then discard the high-order bits.
# Transform using D8 Wavelet to obtain transformed image t:
t = mahotas.daubechies(f,'D8')
# Discard low-order bits:
t /= 8
t = t.astype(np.int8)
print("Fraction of zeros in transform (after division by 8): {0}".format(np.mean(t==0)))
plt.imshow(t)
plt.show()
(Source code, png, hires.png, pdf)
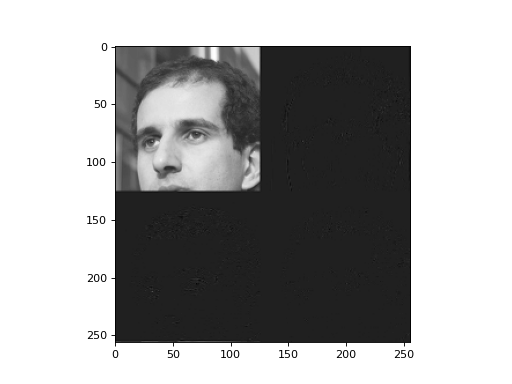
This has 60% zeros! What does the reconstructed image look like?
# Let us look at what this looks like
r = mahotas.idaubechies(t, 'D8')
plt.imshow(r)
plt.show()
(Source code, png, hires.png, pdf)
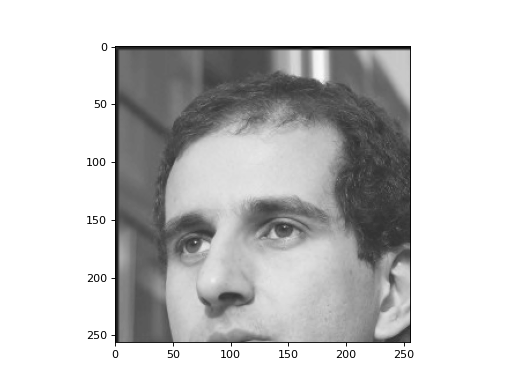
This is a pretty good reduction without much quality loss. We can go further and discard small values in the transformed space. Also, let’s make the remaining values even smaller in magnitude.
Now, this will be 77% of zeros, with the remaining being small values. This image would compress very well as a lossless image and we could reconstruct the full image after transmission. The quality is certainly higher than just keeping every fourth pixel and low-order bits.
tt = soft_threshold(t, 12)
print("Fraction of zeros in transform (after division by 8 & soft thresholding): {0}".format(np.mean(tt==0)))
# Let us look again at what we have:
rt = mahotas.idaubechies(tt, 'D8')
plt.imshow(rt)
(Source code, png, hires.png, pdf)

What About the Borders?¶
In this example, we can see some artifacts at the border. We can use
wavelet_center and wavelet_decenter to handle borders to correctly:
fc = mahotas.wavelet_center(f)
t = mahotas.daubechies(fc, 'D8')
r = mahotas.idaubechies(fc, 'D8')
rd = mahotas.wavelet_decenter(r, fc.shape)
Now, rd is equal (except for rounding) to fc without any border effects.
API Documentation¶
A package for computer vision in Python.
Main Features¶
- features
Compute global and local features (several submodules, include SURF and Haralick features)
- convolve
Convolution and wavelets
- morph
Morphological features. Most are available at the mahotas level, include erode(), dilate()…
- watershed
Seeded watershed implementation
- imread/imsave
read/write image
Documentation: https://mahotas.readthedocs.io/
Citation:
Coelho, Luis Pedro, 2013. Mahotas: Open source software for scriptable computer vision. Journal of Open Research Software, 1:e3, DOI: https://dx.doi.org/10.5334/jors.ac
- mahotas.daubechies(f, code, inline=False)
Daubechies wavelet transform
This function works best if the image sizes are powers of 2!
- Parameters:
- fndarray
2-D image
- codestr
One of ‘D2’, ‘D4’, … ‘D20’
- inlinebool, optional
Whether to write the results to the input image. By default, a new image is returned. Integer images are always converted to floating point and copied.
See also
haarfunction Haar transform (equivalent to D2)
- mahotas.haar(f, preserve_energy=True, inline=False)
Haar transform
- Parameters:
- f2-D ndarray
Input image
- preserve_energybool, optional
Whether to normalise the result so that energy is preserved (the default).
- inlinebool, optional
Whether to write the results to the input image. By default, a new image is returned. Integer images are always converted to floating point and copied.
See also
ihaarfunction Reverse Haar transform
- mahotas.idaubechies(f, code, inline=False)
Daubechies wavelet inverse transform
- Parameters:
- fndarray
2-D image
- codestr
One of ‘D2’, ‘D4’, … ‘D20’
- inlinebool, optional
Whether to write the results to the input image. By default, a new image is returned. Integer images are always converted to floating point and copied.
See also
haarfunction Haar transform (equivalent to D2)
- mahotas.ihaar(f, preserve_energy=True, inline=False)
Reverse Haar transform
ihaar(haar(f))is more or less equal tof(equal, except for possible rounding issues).- Parameters:
- f2-D ndarray
Input image. If it is an integer image, it is converted to floating point (double).
- preserve_energybool, optional
Whether to normalise the result so that energy is preserved (the default).
- inlinebool, optional
Whether to write the results to the input image. By default, a new image is returned. Integer images are always converted to floating point and copied.
- Returns:
- fndarray
See also
haarfunction Forward Haar transform